Extending Non-Equilibrium Pulling Method in GROMACS with Arbitrary User-Defined Atom Weight Factor Expressions
Vedran Miletić, Matea Turalija
😎 Group for Applications and Services on Exascale Research Infrastructure, Faculty of Informatics and Digital Technologies, University of Rijeka
Third Infinity 2022, Max Planck Institute for Multidisciplinary Sciences, Göttingen, 23rd of September 2022
Outline
- Molecular dynamics simulation
- Non-equilibrium pulling
- Uniform flow simulation
- Atom weight factor expression
- Applications
Molecular dynamics simulation
- Simulation of physical movement of atoms and molecules
- Trajectories of atoms and molecules are obtained by solving Newton's equations of motion many times
- Typical time step: 1-2 femtoseconds
- Typical simulated time: nanoseconds to microseconds (10^6 to 10^9 steps)
Non-equilibrium pulling
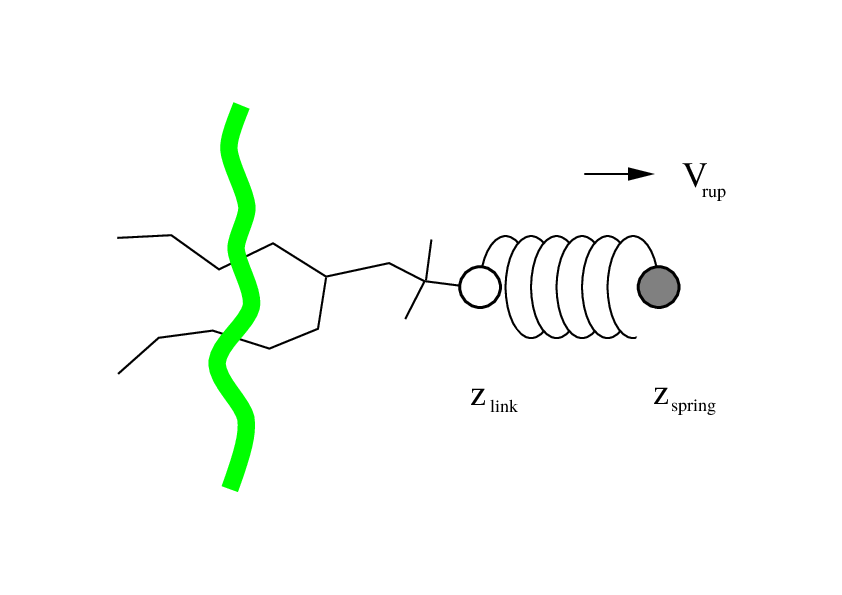
- Applies external force to the molecular system
- Figure source: Non-equilibrium pulling section in the GROMACS Reference Manual
Pull coordinate
- Pull coordinate = distance, angle, or dihedral angle betwen centers of mass of two groups of atoms
- Alternatively, one group can be replaced by a reference position in space
- Combination of coordinates using (optionally time-dependent) expressions: transformation pull coordinate, e.g.
0.5*(x1 + x2)
Pull groups and force
- Pull group = a group of atoms weighted by their mass
- Aditional per-atom weighting factor can be used
- Defined in the simulation parameters, remains the same during simulation
- Aditional per-atom weighting factor can be used
- Constant force pulling applies constant force between the centers of mass of two groups
Processes activated by flow
- Many biological processes occur under flow conditions, e.g.
- Hemostasis to stop bleeding
- Leukocyte adhesion at sites of inflammation
- Spider silk spinning
- The biomolecules involved in the flow-dependent processes undergo specific conformational changes triggered (or influenced) by the flow
Simulating uniform flow (1/3)

- Figure source: File:MD water.gif (Wikimedia Commons)
Simulating uniform flow (2/3)
- Flow is a movement of solvent atoms
- Pulling all solvent atoms works when no other molecules except water are present in the simulation
- Just a slice of solvent molecules should be pulled to allow the solvent atoms to interact with the biomolecule(s) without being "dragged away"
Simulating uniform flow (3/3)

- Figure source: Biophys. J. 116(6), 621–632 (2019). doi:10.1016/j.bpj.2018.12.025
The previous approach (1/4)
- This approach is flow-specific
- Uses atom weighting factors in GROMACS to non-uniformly distribute the pulling force
- Atoms of the solvent inside the slice -> weighting factor is non-zero
- Atoms of the solvent outside the slice -> weighting factor is zero
The previous approach (2/4)
- GROMACS limitation: weighting factors are defined once at the begining of the simulation
- Problem: solvent atoms move during flow simulation, weighting factors should be recomputed each step
- Solution: hack GROMACS to introduce the concept of the slice and recompute atom weighting factors each step
The previous approach (3/4)
-
Each atom is weighted with the weight factor:
\[w_{sp} = x_{unit}^4 - 2x_{unit}^2 + 1\] -
Coordinate \(x\) of each atom in the arbitrary slice is normalized from the interval \([s_{min}, s_{max}]\) to the coordinate \(x_{unit}\) in the interval \([−1, 1]\):
\[x_{unit} = \frac{x - \frac{s_{min} + s_{max}}{2}}{\frac{s_{min} - s_{max}}{2}}\]
The previous approach (4/4)

- Figure source: Biophys. J. 116(6), 621–632 (2019). doi:10.1016/j.bpj.2018.12.025
The new, general approach (1/3)
- Inspired by transformation pull coordinates
- Uses the same fast mathematical expression parser
- Atom weight = dynamic weight factor computed from the expression x weight factor specified in the parameters file x atom mass-derived weight factor
- Dynamic weight factor (and atom weight) recomputed in each simulation step
The new, general approach (2/3)
- Weight factor expression variables:
- Atom position in 3D (
x,y,z) - Atom velocity in 3D (
vx,vy,vz)
- Atom position in 3D (
- Examples:
- Atom weight factor is sum of squares of positions:
x^2 + y^2 + z^2 - Atom weight factor is a linear combination of velocities:
1.75 * vx + 1.5 * vy + 1.25 * vz
- Atom weight factor is sum of squares of positions:
The new, general approach (3/3)
- Covers the requirements of uniform flow simulation
- Non-smooth slice:
x >= 1 && x < 5 ? 1 : 0 - Smooth slice:
x >= 1 && x < 5 ? (x - 2)^4 - 2 * (x - 2)^2 + 1 : 0
Possible applications of atom weight factor expressions
- Simulating uniform flow in arbitrary direction
- Pulling a protein domain with a non-uniform force applied to different residues
- Introducing external force in a subset of the periodic metal/material system
- Your ideas?
Future plans
- Providing the option to configure the number of steps when weight factors are recomputed
- Adding heuristics that avoid recomputation of factors for atoms that did not move or accelerate very much
- Adding time as a variable in the expression
- More extensive testing and physical validation
- Inclusion in a future version of GROMACS (2024?)
Acknowledgments
- Co-author Matea Turalija from GASERI at FIDIT, Uni Rijeka

- Flow-specific approach co-authors Ana Herrera-Rodríguez, Camilo Aponte-Santamaría, and Frauke Gräter from Molecular Biomechanics (MBM) group, Heidelberg Institute for Theoretical Studies (HITS)
How to play with the code
- For non-developers: vedran.miletic.net/#contact
- Group for Applications and Services on Exascale Research Infrastructure (GASERI, 😎): group.miletic.net
- For developers: official GROMACS code repository on GitLab: gitlab.com/gromacs/gromacs
- Check
vm-weight-factor-expressionbranch
- Check
Questions?
GROMACS developer workshop
- Planned ~= spring 2023 (time and location TBA)
- Entry-level development workshop
- Primarily targeted for new developers
- Non-developers interested in exploring development are welcome
- Follow GROMACS forums or @GMX_TWEET for announcements
Author: Vedran Miletić